Это семь фундаментальных математических проблем, учрежденные Математическим институтом Клэя в 2000 году как символ новых вызовов XXI века. Каждая из этих задач представляет собой настоящий интеллектуальный Эверест, за покорение которого назначена награда — один миллион долларов.
«Задачи тысячелетия»: 7 математических проблем, миллион долларов за решение и почему ученые не могут их победить
Что такое «Задачи тысячелетия»?
Проблемы охватывают невероятное количество областей математики:
- алгебраическая и арифметическая геометрия;
- теория чисел и геометрическая топология;
- математическая физика и уравнения в частных производных;
- теоретическая информатика.
Инициатива Института Клэя — продолжение знаменитого списка 23 проблем Давида Гильберта, представленного в 1900 году и определившего развитие математики в XX веке. В отличие от гильбертовских задач, проблемы тысячелетия уже были хорошо известны научному сообществу — многие математики годами безуспешно пытались их решить.
Официальный старт проекту был дан 24 мая 2000 года в парижском Collège de France, где Джон Тейт и Майкл Талия представили эти семь проблем перед международным научным сообществом и бросили мостик между математическими традициями прошлого и вызовами будущего.
Гипотеза Берча и Суиннертона-Дайера
Эта гипотеза, подтвержденная многочисленными экспериментальными данными, устанавливает связь между количеством точек на эллиптической кривой по модулю p и рангом группы ее рациональных точек. Эллиптические кривые (которые описываются кубическими уравнениями с двумя переменными) — это фундаментальные математические объекты и встречаются они много где: от доказательства Великой теоремы Ферма до задач факторизации чисел и современных криптографических систем.
Гипотеза Берча и Суиннертона-Дайера утверждает, что для абелевых многообразий размер группы рациональных точек связан с поведением дзета-функции ζ(s) в окрестности точки s=1. Согласно предположению, если ζ(1)=0, то существует бесконечное множество рациональных точек, тогда как при ζ(1)≠0 их количество конечно. Эта гипотеза — одна из ключевых нерешенных проблем теории чисел.
Исторически математиков всегда привлекала проблема нахождения целочисленных решений уравнений типа x² + y² = z². Евклид полностью описал решения этого уравнения, однако для более сложных случаев они не годятся. В 1970 году Матиясевич доказал неразрешимость десятой проблемы Гильберта и показал, что универсального алгоритма определения существования целочисленных решений произвольных уравнений просто не существует. Но оказалось, что для отдельных классов уравнений прогресс все же возможен.
Гипотеза Ходжа
Эта штука исследует взаимосвязь между топологией множества решений системы алгебраических уравнений и возможностью их описания через другие алгебраические уравнения. В частных случаях (например, при размерности многообразия меньше четырех) гипотеза доказана, однако для четырехмерных пространств проблема остается открытой. Получается, что для проективных алгебраических многообразий (особого семейства «хороших» пространств) так называемые циклы Ходжа — это фактически линейные комбинации алгебраических циклов, имеющих четкую геометрическую природу. Таким образом, гипотеза стремится восстановить связь между абстрактными математическими конструкциями и их геометрическими прообразами.
Уравнения Навье-Стокса
Вообще-то, уравнения, описывающие движение жидкостей и газов — от воды до воздуха — были сформулированы еще в XIX веке, однако есть ряд еще открытых вопросов. Математики до сих пор не могут строго доказать существование и единственность решений даже для базовых сценариев. А доказать было бы славно, потому что понимание свойств решений позволило бы объяснять и прогнозировать природные явления — от легкого бриза до сложных турбулентных потоков, которые сопровождают полет самолета или движение корабля.
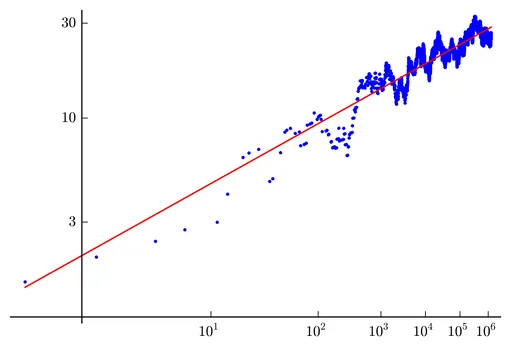
Проблема P против NP
Речь идет о проблеме равенства классов сложности NP и P или, так называемой, проблеме перебора. Суть этой фундаментальной задачи информатики можно выразить простым вопросом: если решение задачи легко проверить, означает ли это, что найти его — это тоже легко? Классический пример — задача о гамильтоновом пути.
Нужно посетить N городов, не возвращаясь в уже посещенные. Проверить готовый маршрут просто, но найти его с нуля — невероятно сложно! Разберем на более приземленном примере. Представьте, что нужно расселить 100 студентов из 400 претендентов в общежитие, учитывая список «несовместимых» пар от деканата. Проверить корректность готового списка легко, но подобрать его вручную практически невозможно.
Проблему сформулировали Стивен Кук и Леонид Левин независимо друг от друга в 1971 году. Ее решение не только определило бы границы возможностей вычислений, но и крепко встряхнуло бы криптографию, искусственный интеллект и методы оптимизации.
Гипотеза Римана
Простыми числами (2, 3, 5, 7...) считаются числа, которые делятся только на единицу и самих себя. Их распределение среди натуральных чисел кажется хаотичным, однако немецкий математик Бернхард Риман в 1859 году обнаружил связь между частотой появления простых чисел и поведением дзета-функцииζ(s) — сложной математической функции, задаваемой рядом 1 + 1/2ˢ + 1/3ˢ + ...
Все нетривиальные нули дзета-функции (то есть комплексные решения уравнения ζ(s) = 0) должны лежать на вертикальной прямой с действительной частью 1/2. Итак, что это нам дает?
- Гипотеза подтверждена для первых 10 триллионов решений.
- Если она верна для всех случаев, это раскроет закономерности распределения простых чисел.
- Теорема о простых числах описывает их среднее распределение, а гипотеза Римана уточняет отклонения от этого среднего.
Надо ли объяснять, что доказательство этой гипотезы позволило бы совершить прорыв в целой куче областей — от криптографии и теории чисел до понимания самих свойств простых чисел.
Теория Янга-Миллса
Разработанная полвека назад теория Янга-Миллса стала математическим фундаментом современной физики элементарных частиц. Хотя ее предсказания многократно подтверждены экспериментально, строгого математического обоснования до сих пор нет.
Дело в том, что для корректного описания сильных взаимодействий частиц теория требует существования «массовой щели» — свойства, которое объясняет почему квантовые частицы обладают массой, хотя соответствующие классические волны распространяются со скоростью света. Решение этой проблемы укрепит теоретические основы квантовой теории поля, а человек сможет глубже осознать природу материи.
Гипотеза Пуанкаре: единственная решенная из «Задач тысячелетия»
На заре XX столетия, в 1904 году, Анри Пуанкаре сформулировал фундаментальный вопрос топологии: трехмерная сфера это единственное трехмерное многообразие? Проще говоря, если любая петля на поверхности может быть стянута в точку (как резинка на яблоке), означает ли это, что эта поверхность — обязательно именно сфера? Для двумерного случая ответ был известен, а вот трехмерный вариант оставался неразрешенным почти век, пока... за задачу не взялся Григорий Перельман.
В 2002-2003 годах он опубликовал доказательство, в котором использовал теорию потока Риччи. его работа не только подтвердила гипотезу Пуанкаре, но и доказала более общую гипотезу геометризации Терстона, которая описывала структуру всех трехмерных многообразий. Это значит, что любое трехмерное многообразие можно разложить на стандартные геометрические фрагменты. Это решило одну из величайших проблем математики XX века и принесло Перельману мировое признание и... отказ от Филдсовской премии.
Семь задач тысячелетия остаются символами интеллектуального предела человечества. Несмотря на развитие математического аппарата и технический прогресс, шесть из семи «Эверестов» науки все еще не поддаются объяснению. Это — очередное напоминание о величии и глубине мира математики.